通信制高校
通信制高校 一ツ葉高校 
キャンパス紹介 解答Part.2！！
通信制高校 一ツ葉高校福岡キャンパス 山本です。
今日もとてもいい天気となりました！
みなさんいかがお過ごしでしょうか？
今週は、天気のいい一週間でした。春休みの生徒は、何をして過ごしてましたか？
旅行に行ったり、家でゆっくりしたり～
それぞれ、春休みを満喫している事でしょう。
今回は、お待ちかね？の
『解けるかな？？Part.2！』の解説をですよ～！！
今回のは、少し難しかったですかね・・・？数学では、有名な問題なので一度でも聞いたことある人は、分かったかもしれません。
では、まずは正解から
正解は・・・987通りです！
えーー！！そんな数えられないよ～って思った方！その通りです！フツ―に一つ一つ考えるととてつもない時間がかかります。ポイントは、法則を見つけることですね！
以下が解説です。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
階段が1段だとすると登り方は、1通りしかありません。これは簡単ですね！
次に階段が2段だとすると、1段ずつ登る方法と一気に1段飛ばして登る方法の2通りがあります。写真を参考に↓
そして、階段が3段だとすると・・・
文章では、分かりにくいので写真で↓
よって、3通りあります。
ここまで理解できましたか？
3段まで考えた時、あることに気付いた人は素晴らしいですね！
では、4段まで増やして考えてみましょう！！
4段だと・・・
よって、5通りあります。
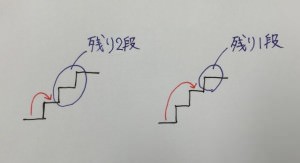
ここで、3段について少し違う目線で考えてみましょう。
もし、最初に1段登ったとすると残りは・・・2段。
もし、最初に1段飛ばしで登ったとすると残りは・・・1段。
あれ？？？残りの階段の登り方は、2段の場合と1段の場合でそれぞれ2通り、1通りなので、
3段の場合の登り方=2段の場合の登り方＋1段の場合の登り方
で求めることができます。
ということは、4段の場合も同じように考えると、
もし、最初に1段登ったとすると残りは・・・3段。
もし、最初に1段飛ばしで登ったとすると残りは・・・2段。
すなわち、
4段の場合の登り方=3段の場合の登り方＋2段の場合の登り方
で求めることができます。
つまり、前2つの通り数を次々足していけば答えが出るという訳です。
どうでしたか？すっきりしましたか？もやもや・・・？？
今回のブログは少し長くなってしまいました。
最後まで読んで頂き、ありがとうございました！
通信制高校 一ツ葉高校福岡キャンパス 山本
通信制高校 一ツ葉高校福岡キャンパス 山本です。
今日もとてもいい天気となりました！
みなさんいかがお過ごしでしょうか？
今週は、天気のいい一週間でした。春休みの生徒は、何をして過ごしてましたか？
旅行に行ったり、家でゆっくりしたり～
それぞれ、春休みを満喫している事でしょう。
今回は、お待ちかね？の
『解けるかな？？Part.2！』の解説をですよ～！！
今回のは、少し難しかったですかね・・・？数学では、有名な問題なので一度でも聞いたことある人は、分かったかもしれません。
では、まずは正解から
正解は・・・987通りです！
えーー！！そんな数えられないよ～って思った方！その通りです！フツ―に一つ一つ考えるととてつもない時間がかかります。ポイントは、法則を見つけることですね！
以下が解説です。
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
階段が1段だとすると登り方は、1通りしかありません。これは簡単ですね！
次に階段が2段だとすると、1段ずつ登る方法と一気に1段飛ばして登る方法の2通りがあります。写真を参考に↓
そして、階段が3段だとすると・・・
文章では、分かりにくいので写真で↓
よって、3通りあります。
ここまで理解できましたか？
3段まで考えた時、あることに気付いた人は素晴らしいですね！
では、4段まで増やして考えてみましょう！！
4段だと・・・
よって、5通りあります。
ここで、3段について少し違う目線で考えてみましょう。
もし、最初に1段登ったとすると残りは・・・2段。
もし、最初に1段飛ばしで登ったとすると残りは・・・1段。
あれ？？？残りの階段の登り方は、2段の場合と1段の場合でそれぞれ2通り、1通りなので、
3段の場合の登り方=2段の場合の登り方＋1段の場合の登り方
で求めることができます。
ということは、4段の場合も同じように考えると、
もし、最初に1段登ったとすると残りは・・・3段。
もし、最初に1段飛ばしで登ったとすると残りは・・・2段。
すなわち、
4段の場合の登り方=3段の場合の登り方＋2段の場合の登り方
で求めることができます。
つまり、前2つの通り数を次々足していけば答えが出るという訳です。
どうでしたか？すっきりしましたか？もやもや・・・？？
今回のブログは少し長くなってしまいました。
最後まで読んで頂き、ありがとうございました！
|
段数 |
1段 |
2段 |
3段 |
4段 |
5段 |
6段 |
7段 |
8段 |
9段 |
10段 |
11段 |
12段 |
13段 |
14段 |
15段 |
|
通り数 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
144 |
233 |
377 |
610 |
987 |
通信制高校 一ツ葉高校福岡キャンパス 山本
博多キャンパス 
0120-277-128